Answer:
Steve will take 240 minutes or 4 hours.
Step-by-step explanation:
Steve and Hillary can mow a lawn in 60 minutes by working together. However, Hillary works three times faster than Steve.
Let's assume Steve takes takes x minutes to mow alone.
This implies that Hillary can mow alone in x/3 minutes.
In a minute, Steve can mow 1/x of the lawn, so this means Hillary can mow 3/x of the lawn.
In a minute together then can mow,
=
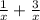
=
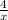
In 60 minutes they can mow
=
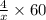
=
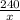
This means that it takes 4 hours for Steve to mow the lawn alone.