Question

suppose that the man pictured on the front side is orbiting the earth (mass=5.98 x 10^24kg at a distance of 310 miles above the surface of the earth (radius=400 miles)

Answer 1

The question is about the orbital motion of a man pictured on the front side while he is orbiting the Earth. We can use the concepts of gravitational force and centripetal force to answer this question. To calculate the orbital speed of the man, we can use the formula v = sqrt(GM/r).

Step-by-step explanation:

The question is about the orbital motion of a man pictured on the front side while he is orbiting the Earth. To answer this question, we can use the concepts of gravitational force and centripetal force.

The man is orbiting the Earth at a distance of 310 miles above the surface. We know that the mass of the Earth is 5.98 x 10^24 kg and its radius is 400 miles.

To calculate the orbital speed of the man, we can use the formula v = sqrt(GM/r), where G is the gravitational constant, M is the mass of the Earth, and r is the distance from the center of the Earth.

Using this formula, we can calculate the orbital speed of the man.

Answer 2

a = 9.81[m/s^2]; v = 18683.5[m/s]

Step-by-step explanation:

The stament of the problem is:

Suppose that the man pictured on the front side is orbiting the earth (mass = 5.98 x 1024kg) at a distance of 310 miles (1600 meters = 1 mile) above the surface of the earth (radius = 4000 miles).

a. What acceleration does he experience due to the earth's pull?

b. What tangential velocity must he possess in order that he orbit safely (in m/s)?

First we need to convert all the initial data to units of the SI

Rs = 310 [mil] = 498897 [m]

RT= 400 [mil] = 643738 [m]

r = Rs + RT = 1142635 [m] "distance from the center of the earth to the man"

`F=G*(M*m)/(r^(2) ) \\where:\\`

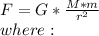
G = universal gravitational constant

M = mass of the earth [kg]

m = mass of the man [kg]

r = distance from the center of the earth to the man [m]

a)

The acceleration he is experimenting is the same acceleration given by the gravity, therefore:

a = g = 9.81[m/s^2]

b)

To find the tangential velocity, we must determinate the force exerted by the earth.

Now we will find the force exerted by the gravity when the man is orbiting the earth at distance r.

`G = 6.67*10^(-11) [(N*m^(2) )/(kg^(2) ) ]\\M=5.98*10^(24)[kg]\\ m=100 [kg]\\Replacing:\\F = G*(M*m)/(r^(2) )`

`F = 6.67*10^(-11)*(5.98*10^(24)*100 )/(1142635^(2) ) \\ F= 30550 [N]`

And this force will be equal to the following expression:

`F = m*(v^(2) )/(r) \\where:\\v= tangential velocity [m/s]\\v=\sqrt{(F*r)/(m) } \\v=\sqrt{(30550*1142635)/(100) } \\v=18683.5[m/s]`