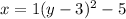Answer:
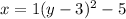
Explanation:
we need to find the equation of the parabola with vertex (-5,3), with axis parallel to the x-axis.
general equation of horizontal parabola is

where (h,k) is the vertex
(-5,3) is the vertex. h=-5 and k=3. plug in the values in the general equation
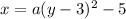
Now find out the value of 'a' using x intercept (4,0)

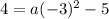
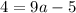
Add 5 on both sides
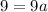
a=1
the equation becomes