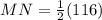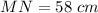Answer:
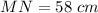
Explanation:
we know that
The Midpoint Theorem states that the segment joining two sides of a triangle at the midpoints of those sides is parallel to the third side and is half the length of the third side
In this problem
M is the mid-point segment AB
N is the mid-point segment BC
so
Applying the Midpoint Theorem
MN is parallel to AC
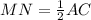
we have that
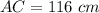 ---> given problem
---> given problem
substitute