Question

When positive integer k is divided by 5, the remainder is 2. When k is divided by 6, the remainder is 5. If k is less than 40, what is the remainder when k is divided by 7?

Answer 1

Remainder: 3

Explanation:

We have been given that when positive integer k is divided by 5, the remainder is 2. We can represent this information in an equation as:

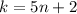`k=5n+2`, where n represents quotient.

From this equation we will get possible values of k less than 40 as: {2, 7, 12, 17, 22, 27, 32, 37}

We are also told that when k is divided by 6, the remainder is 5. We can represent this information in an equation as:

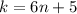`k=6n+5`, where n represents quotient.

From this equation we will get possible values of k less than 40 as: {5, 11, 17, 23, 29, 35}

We can see from our both sets that 17 is common number, therefore, value of k is 17.

Let us divide 17 by 7 to find our required remainder as:

`(17)/(7)=(14+3)/(7)=2+(3)/(7)`

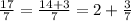
Therefore, the remainder would be 3, when k is divided by 7.