Question

What information about water is needed to calculate the enthalpy change for converting 1 molmol H2OH2O(gg) at 100 ∘C∘C to H2OH2O(ll) at 80 ∘C∘C?

Answer 1

Answer: The enthalpy change for the given process is -42.3 kJ/mol

Step-by-step explanation:

The processes involved in the given problem are:

`1.)H_2O(g)(100^oC)\rightarrow H_2O(l)(100^oC)\\2.)H_2O(l)(100^oC)\rightarrow H_2O(l)(80^oC)`

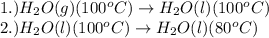
Pressure is taken as constant.

To calculate the amount of heat released at same temperature, we use the equation:

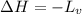`\Delta H=-L_(v)` ......(1)

where,

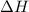`\Delta H` = enthalpy change

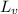`L_(v)` = latent heat of vaporization

To calculate the amount of heat absorbed at different temperature, we use the equation:

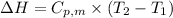`\Delta H=C_(p,m)* (T_(2)-T_(1))` .......(2)

where,

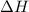`\Delta H` = enthalpy change

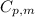`C_(p,m)` = specific heat capacity of medium

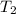`T_2` = final temperature

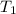`T_1` = initial temperature

Calculating the enthalpy for each process:

• For process 1:

We are given:

`L_v=40.79kJ/mol=40790J/mol`

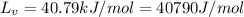
Putting values in equation 1, we get:

`\Delta H_1=-40790J/mol`

• For process 2:

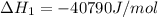
We are given:

`C_(p,l)=75.3J/mol.^oC\\T_1=100^oC\\T_2=80^oC`

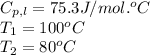
Putting values in equation 2, we get:

`\Delta H_2=75.3J/mol.^oC* (80-(100))^oC\\\\\Delta H_2=-1506J/mol`

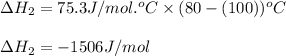
Enthalpy change of the reaction =
`\Delta H_1+\Delta H_2`

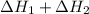
Enthalpy change of the reaction =
`[-40790+-1506]J/mol=-42296J/mol=-42.3kJ/mol`

Hence, the enthalpy change for the given process is -42.3 kJ/mol