Question

The area of triangle ABC is 3√2 square inches. Find the measure of the acute angle, A, if b = 9 meters and c = 2 meters.

Answer 1

`A\approx 28^(\circ)`

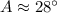
Explanation:

Please find the attachment.

We have been given that area of triangle ABC is 3√2 square inches.

`\text{Area}=(1)/(2)\text{Base}* \text{height}`

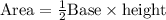
We know that area of triangle an be found using trigonometry as:

`\text{Area}=(1)/(2)* c* h`

`\text{sin}(A)=(h)/(9)\\h=9\cdot \text{sin}(A)`

`3√(2)=(1)/(2)* 2* 9\cdot \text{sin}(A)`

`3√(2)=9\cdot \text{sin}(A)`

`9\cdot \text{sin}(A)=3√(2)`

`\text{sin}(A)=(3√(2))/(9)`

`\text{sin}(A)=(√(2))/(3)`

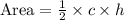
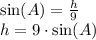
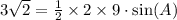
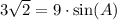
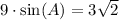
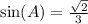
Now, we will use inverse sine to find the value of angle A as:

`A=\text{sin}^(-1)((√(2))/(3))`

`A=28.1255057^(\circ)`

`A\approx 28^(\circ)`

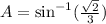
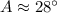
Therefore, the measure of angle A is approximately 28 degrees.