Question

At what values of x does f(x) = x^3 - 2x^2 -4x+1 satisfy the mean value theorwm on [0,1]

Answer 1

x=1/3

Explanation:

A function f is given as

`f(x) = x^3-2x^2-4x+1` in the interval [0,1]

This function f being an algebraic polynomial is continuous in the interval [0,1] and also f is differntiable in the open interval (0,1)

Hence mean value theorem applies for f in the given interval

`f(1) = 1-2-4+1 = -4\\f(0) = 1`

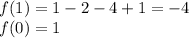
The value

`(f(1)-f(0))/(1-0) =(-4-1)/(1) =-5`

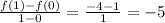
Find derivative for f

`f'(x) = 3x^2-4x-4`

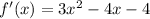
Equate this to -5 to check mean value theorem

`3x^2-4x-4=-5\\3x^2-4x+1=0\\\\(x-1)(3x-1) =0\\x= 1/3 : x = 1`

We find that 1/3 lies inside the interval (0,1)