Answer:
Option A. -(
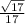 )
)
Explanation:
Equation of a given line is a + 4b = 0 or b = -
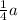
This in the form of y = mx + b, which is slope-intercept form.
Here slope of the line is (
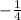 ).
).
Or tanθ =
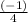
This line coincides with the terminal side of the angle in standard position where cosθ > 0
Since tanθ =
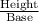
and sinθ =

Hypotenuse =
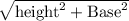
=

=
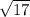
Since tanθ is negative and cosθ > 0 that means θ lie in fourth quadrant.
Therefore, sinθ will be negative.
[
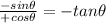 ]
]
sinθ = -
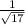
= -
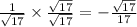
Answer will be option A.