Answer:
NOO!
Explanation:
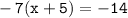
First ,let's move all terms to the left:

Add all numbers together, and all variables
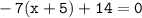
Multiply parentheses:-
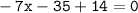
Add all numbers/variables together:
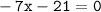
Now, move all terms containing x to the left, and all other terms to the right:
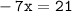
Divide both sides by -7:-
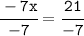
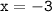
Nope, 10 isn't a solution to -7(x+5)=-14.
~