Question

Matt needs to put a fence around a garden in his backyard. The perimeter is 104 meters. The length is 6 meters more than the width.

Matt wrote the first let statement. Fill in the blank below to complete the second let statement.
Let w = the width
Let = the length
Write an equation below that Matt can use to find the length and the width and solve it. What are the dimensions of the garden?

Answer 1

The equation is
`Perimeter=2(2w+6)`.

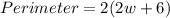The length is 29 m and width is 23 m of the garden.

Explanation:

Given,

Perimeter = 104 m

Solution,

Let 'w' = the width

Let 'l' = the length

Since the garden is in the form of rectangle.

Now we know that the perimeter of rectangle is 2 times the sum of length and width.

We can frame it as;

`Perimeter=2(l+w)`

According to question, the length is 6 meters more than the width.

So we can say that;

`l=w+6`

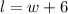
Now we substitute the value of 'l' and get;

`Perimeter=2(l+w)=2(w+6+w)=2(2w+6)`

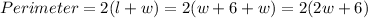
Hence The equation is
`Perimeter=2(2w+6)`.

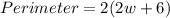Now we solve the equation by putting the values and get;

`2(2w+6)=104\\\\2w+6=(104)/(2)=52\\\\2w=52-6=46\\\\w=(46)/(2)=23\ m`

`l=w+6=23+6=29\ m`

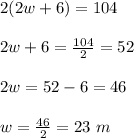
Hence The length is 29 m and width is 23 m of the garden.