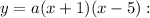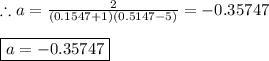Answer:
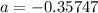
Explanation:
We know that all the vertices of the isosceles trapezoid lie on the parabola, and the points A and D lie along the x-axis, i.e at

Therefore points A and D are located where
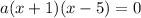
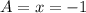
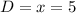
Now we need to find the coordinates of point C; we already have its y-coordinate (it's
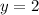 ), and looking at the figure attached we see that the x-coordinate of point C is
), and looking at the figure attached we see that the x-coordinate of point C is
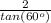 farthar from the coordinate of point C; thus
farthar from the coordinate of point C; thus
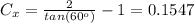
Therefore the coordinates of C are
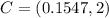
Now this point C lies on the parabola, and therefore must satisfy the equation