3p + 7d = 98.75 and 15p + 6d = 218.25 are the system of equations that can be used to find the price of one bag of popcorn and the price of one drink
The price of 1 drink is $ 9.5
Solution:
Let "p" be the price of 1 bag of popcorn
Let "d" be the price of 1 drink
Given that,
Sophia spends a total of $98.75 on 3 bags of popcorn and 7 drinks
Therefore, we can frame a equation as,
3 x price of 1 bag of popcorn + 7 x price of 1 drink = 98.75
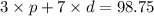
3p + 7d = 98.75 -------- eqn 1
Skylar spends a total of $218.25 on 15 bags of popcorn and 6 drinks
15 x price of 1 bag of popcorn + 6 x price of 1 drink = 218.25
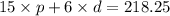
15p + 6d = 218.25 -------- eqn 2
Thus eqn 1 and eqn 2 are the system of equations that can be used to find the price of one bag of popcorn and the price of one drink
Determine and state the price of a drink:
Let us solve eqn 1 and eqn 2
Multiply eqn 1 by 5
15p + 35d = 493.75 ------ eqn 3
Subtract eqn 2 from eqn 3
15p + 35d = 493.75
15p + 6d = 218.25
( - ) -------------------------------
29d = 275.5
d = 9.5
Substitute d = 9.5 in eqn 1
3p + 7(9.5) = 98.75
3p + 66.5 = 98.75
3p = 32.25
p = 10.75
Thus the price of 1 drink is $ 9.5