Answer: OPTION B.
Explanation:
The equation of a line that passes through the origin has this form:
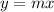
Where "m" is the slope of the line.
By, definition, Proportional relationships have the following form:
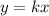
Where "k" is the Constant of proportionality.
Therefore, the graph of a Proportional relationship is a straight line that passes through the origin. Then:
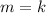
As you can observe in the picture attached, if you connect the ordered pairs shown in the graph, you get a line that does not pass through the origin.
Therefore, you can conclude that the relationship between those two quantities is not proportional.