Question

6. A point on the unit circle lies on the terminal side of an angle in standard position in quadrant l. whether each measurement is positive or negative.

the cosine of the angle is : positive or negative

the sine of the angle is: positive or negative

please help !!! show work
thank you

Answer 1

5. arc length = radius x central angle in radians

arc length = 28 x 3π/4 = 21π

answer: (21π) cm

6. You are right. Quadrant 1 features points where both the x coordinate and the y coordinate are positive. Cosine and sine are basically special coordinates.

7. We need to find the tan(2π/3). The hint is quite bad I must say because you need to find the sine and cosine of an angle to find tangent. Okay, back to the problem.

tan(2π/3) = sin(2π/3)/cos(2π/3)

We know π/3 to be a special angle on the unit circle. It has a cosine of 1/2 and a sine of
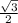`(√(3) )/(2)`. Because we know this, its partner in quadrant 2 (2π/3) will have a cosine of -1/2 and a sine of
`(√(3) )/(2)`.

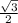tan(2π/3) =
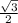`(√(3) )/(2)` ÷ -1/2= -√3

answer: -√3

8. Both angles are special angles so...

2cos(π/6) - 2tan(π/3) = 2(
`(√(3) )/(2)`) - 2(
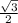`(√(3) )/(2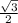)` ÷ 1/2) = √3 - 2√3 = -√3 (ok what a coincidence)

answer: -√3