Question

Both circle Q and circle R have a central angle measuring 75°. The ratio of circle Q's radius to circle R's radius is 3 4 . Which ratio represents the area of the sector for circle Q to the area of the sector for circle R? A) 16 9 B) 2 5 C) 3 4 D) 9 16

Answer 1

D) 9 : 16

Explanation:

Given,

Central angle for circle Q = Central angle for circle R = 75°

Ratio of the radii of circle Q to circle R =
`(3)/(4)`

We have to find the ratio of the areas of the sector for circle Q to the sector for circle R.

Solution,

Since we know that the formula for Area of sector is
`(\pi r^2\theta)/(360)`.

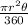So the ratio of the areas of sectors for circle Q to circle R;

`Ratio=((\pi r_1^2\theta)/(360))/((\pi r_2^2\theta)/(360))`

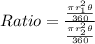
Here the central angle(θ) is equal for both circles.

And also π and 360° is equal, so we can cancel it.

Now,

`Ratio = (r_1^2)/(r_2^2)`

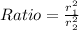
Since the ratio of the radii of circle Q to circle R =
`(3)/(4)`

We can also say that
`(r_1)/(r_2)=(3)/(4)`

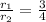
Now we substitute the value of
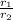`(r_1)/(r_2)` and get;

`Ratio=((3)/(4))^2=(3^2)/(4^2)=(9)/(16)`

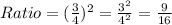
Hence The ratio of the area of the sector for circle Q to the area of the sector for circle R is 9:16.