Question

How much power is required to raise 2 kilograms 3 meters in 4 seconds?

Answer 1

Power = 14.7 W

Step-by-step explanation:

Given:

Mass of the object to be raised is,
`m=2\ kg`

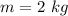
Height to be raised is,
`h=3\ m`

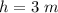
Time taken during the work is,
`t=4\ s`

As the object is raised vertically, the acceleration acting on it is due to gravity and is equal to 9.8 m/s².

Now, work done in moving an object of mass 'm' to a height 'h' is given as:

`Work=mgh`

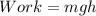
Now, power is given as the rate of doing work which is given as:

`Power=(Work)/(TIme)\\\\Power=(mgh)/(t)\\`

Now, plug in all the values and solve for power. This gives,

`Power=(2*9.8*3)/(4)\\\\Power=(58.8)/(4)\\\\Power=14.7\ W`

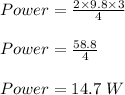
Therefore, the power required to raise the object to a height of 3 meters is 14.7 watts.