Question

Find the distance from the point (6, - 7) to the line x + 7y = 7

Answer 1

`√(50)`

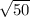
Explanation:

Step 1: Put the line in slope intercept form,

`x + 7y = 7`

`7y = - x + 7`

`y = - (x)/(7) + 1`

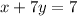
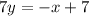
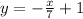
Step 2: The line that contains the point must be perpendicular to the original line.

So the slope of this line must be 7, and pass through (6,-7).

So we have

`y + 7 = 7(x - 6)`

`y + 7 = 7x - 42`

`y = 7x - 49`

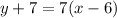
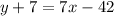
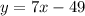
Step 3: Find where the lines intersect at:

Now, we set that equal to -x/7+1

`( - x)/(7) + 1 = 7x - 49`

`- x + 7 = 49x - 343`

`350 = 50x`

`7 = x`

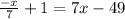
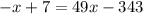
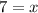
So the two lines intersect at (7,y).

To find y, plug in 7 for any function

`( - 7)/(7) + 1 = 0`

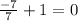
So y=0.

So the two lines intersect at (7,0).

Step 4: Use distance formula,

Find the distance between (7,0) and (6,-7).

`d = \sqrt{ (- 7 - 0) {}^(2) + (6 - 7) {}^(2) }`

`d = \sqrt{ - 7) {}^(2) + ( - 1) {}^(2) }`

`d = √(50)`

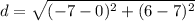
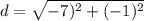
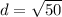
So the distance to the line root of 50.