Question

On a coordinate plane, a dashed straight line has a negative slope and goes through (0, 3) and (2, negative 1). Everything to the left of the line is shaded. Which linear inequality is represented by the graph? y > 2x + 3 y < 2x + 3 y > −2x + 3 y < −2x + 3

Answer 1

`y<-2x+3`

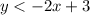
Explanation:

First, we use the given points to find the slope of such line.

The formula to find the slope is

`m=(y_(2) -y_(1) )/(x_(2) -x_(1) )`

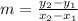
In this case, the points are (0,3) and (2,-1).

`m=(-1-3)/(2-0)=-(4)/(2)=-2`

Then, we use the point-slope formula to find the equation

`y-y_(1) =m(x-x_(1) )\\y-3=-2(x-0)\\y=-2x+3`

Now, notice that everything to the left of the line is shaded, that means the origin must be part of the solutions.

Therefore, the right inequality is

`y<-2x+3`

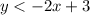
(The image attached shows the graph)

Answer 2

The answer to your question is y < -2x + 3

Explanation:

See the graph below

Process

1.- Find the slope

`m = (y2 - y1)/(x2 - x1)`

Substitution

`m = (-1 - 3)/(2 - 0)`

`m = (-4)/(2)`

`m = -2`

2.- Find the equation of the line

y - y1 = m(x - x1)

Substitution

y - 3 = -2(x - 0)

Simplify and solve for y

y - 3 = -2x

y = -2x + 3

3.- Write the inequality

As the left area of the plane is shaded the inequality must be

y < -2x + 3