Question

Find (ƒ • g)(x) where ƒ(x) = x2 + 2, g(x) = x – 3.

Answer 1

`\text{The value of } (f.g)(x) \text{ is }(f * g)(x) =x^3-3x^2+2x-6`

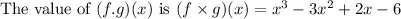
Solution:

Given that:

`f(x) = x^2+2`

`g(x) = x - 3`

We have to find (f . g)(x)

The formula for (f . g)(x) is given as:

`(f * g)(x) = (f (x))(g(x))`

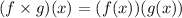
Substitute the given functions f(x) and g(x)

`(f * g)(x) =(x^2+2)(x-3)`

Multiply both functions

Multiply each term in first bracket with each terms in second bracket

`(f * g)(x) = (x^2)(x)-3(x^2)+2(x) + 2(-3)\\\\(f * g)(x) =x^3-3x^2+2x-6`

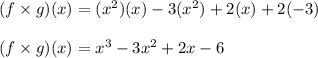
Thus the value of (f .g)(x) is found