Answer:
y ≤
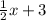
Explanation:
Since everything below and to the right of the line is shaded, we must have the following:
y ≤
because the symbol ≤ implies that the area below the line is the shaded part
with this, options 3 and 4 are discarded
now, on the right side of the symbol we should have the expression for a line, which as a general form:
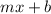
where m is the slope and b is the y-intercept of the line
so until now the answer should be in the form
y ≤
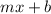
and we calculate the slope m with the two points we are given:
(-4, 1) and (0, 3)
where:
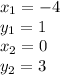
and we plug this values in the slope equation:

so now we know that our solution must have the form:
y ≤
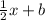
and b can be found since we know that the line passes through (0, 3), so when x=0 y=3, this means that the y-intercept b is 3:
y ≤
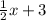
which is the second option