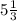Question

What is the value of a?
5 units
5 1/3 units
6 2/3 units
7 units

Answer 1

Value of a =
`5 (1)/(3)`

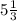
Step-by-step explanation:

This complete Question can be solved via Pythagoras Theorem.

Pythagoras Theorem says that in a right angled triangle, the square of the side which is opposite to the right angle is equal to the squares of both adjacent sides which make the right angle.

So in the given figure, considering triangle XZW, right angled at W,
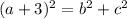`(a+3)^(2) = b^(2) + c^(2)`. Consider this as Equation 1

Also Considering triangle WYZ right angled at Y,
`c^(2) = 3^(2) + 4^(2)`, and hence we can calculate the value of c =
`√(9+16)` =
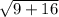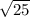`√(25)` = 5

Considering triangle WXY right angled at Y,
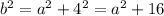`b^2 = a^2 + 4^2 = a^2 + 16`. Consider this as Equation 2.

Substituting value of c in Equation 1, we get as follows:

`(a+3)^(2) = b^(2) + c^(2)`

`(a+3)^(2) = b^(2) + 5^(2)`

`(a+3)^(2) = b^(2) + 25`

`a^2 + 3^2 + 2 * a * 3 = b^(2) + 25`

`a^2 + 9 + 6 * a = b^(2) + 25`

`a^2 + 6 * a = b^(2) + 25-9`

`a^2 + 6 * a = b^(2) + 16`

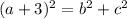
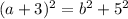
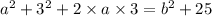
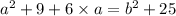
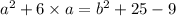
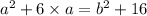
Consider this as Equation 3

Substituting Equation 2 in Equation 3.

`a^2 + 6 * a = a^2 + 16 + 16`

`+ 6 * a = 32`

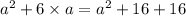
Hence a =
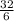`(32)/(6)` =
`5 (1)/(3)`