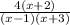Question

Multiply

show your work

2(2+3) 4x(x+2)
----------- × -------------
x(x-1) 10(x+3)​

Answer 1

The product of given two fractions is

`(4(x+2))/((x-1)(x+3))`

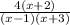
Therefore
`(2(2+3))/(x(x-1))* (4x(x+2))/(10(x+3))=(4(x+2))/((x-1)(x+3))`

Explanation:

Given expression is

`(2(2+3))/(x(x-1))* (4x(x+2))/(10(x+3))`

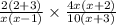
To find the product of two given fractions as below :

`(2(2+3))/(x(x-1))* (4x(x+2))/(10(x+3))=(2(5))/(x(x-1))* (2x(x+2))/(5(x+3))`

`=(10)/(x(x-1))* (2x(x+2))/(5(x+3))`

`=(20x(x+2))/(5x(x-1)(x+3))`

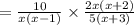
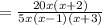
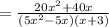`=(20x^2+40x)/((5x^2-5x)(x+3))` (multiply each term in the factor to each term in the another factor )

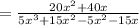`=(20x^2+40x)/(5x^3+15x^2-5x^2-15x)` ( adding the like terms )

`=(20x^2+40x)/(5x^3+10x^2-15x)`

`=(5x(4x+8))/(5x(x^2+2x-3))`

`=(4(x+2))/((x-1)(x+3))`

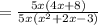
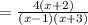
Therefore
`(2(2+3))/(x(x-1))* (4x(x+2))/(10(x+3))=(4(x+2))/((x-1)(x+3))`

Therefore the product of given two fractions is
`(4(x+2))/((x-1)(x+3))`