Question

A bowl contains 25 balls numbered 1 to 25. A ball is drawn and its number is noted. Without replacing the first ball, another ball is drawn.

The probability that the numbers on both balls are odd numbers is
Reset
Next

Answer 1

13/50

explanation is plato

Answer 2

The probability that the numbers on both balls are odd numbers is
`(13)/(50)`

Solution:

The probability of an event is given as:

`probability =\frac{\text { number of favorable outcomes }}{\text { total number of possible outcomes }}`

Given that, bowl contains 25 balls numbered 1 to 25

The sample space is given as;

{ 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25 }

Therefore,

Total number of possible outcomes = 25

A ball is drawn and its number is noted. Without replacing the first ball, another ball is drawn.

Numbers on both balls are odd numbers

Let us first find the probability that first ball is odd

Favorable outcome = odd numbers

Favorable outcome = 1, 3, 5, 7, 9, 11, 13, 15, 17, 19, 21, 23, 25

Number of favorable outcomes = 13

Thus, probability is given as:

`probability = (13)/(25)`

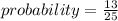
Now Without replacing the first ball, another ball is drawn.

Find the probability that second ball is odd number

Without replacing means that ball is not put back into bowl

So, sample space = 25 - 1 = 24

Total number of possible outcomes = 25

Number of favorable outcomes = 13 - 1 = 12

Thus, probability is given as:

`probability = (12)/(24)`

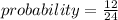
Probability that the numbers on both balls are odd numbers is:

Multiply both the probabilities

`\text{ probability of odd } = (13)/(25) * (12)/(24) = (13)/(50)`

Thus, probability that the numbers on both balls are odd numbers is
`(13)/(50)`