Question

Consider the three points (-7, -7), (21, 14), (49, 35)

Part A: Which of the following points are on the same line that passes through the (-7, -7), (21, 14), (49, 35)? Select all that apply.
A. (5, 9)
B. (5, 2)
C. (17, 11)
D. (4,3)
E. (33,23)
Part B: Show or explain how you determined which points were on the line and which were not on the line.

Answer 1

Part a) B (5,2) and E (33,23) lie on the line

A (5,9) ,C. (17, 11) and D. (4,3) do not lie on the line.

Part b) By substituting the given point into the equation of the line going through (-7, -7), (21,14), (49, 35).

Explanation:

Given the three points (-7, -7), (21,14), (49, 35);

We find the slope using:

`m = (y_2-y_1)/(x_2-x_1)`

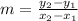
Find the slope using (-7, -7) and (21, 14), we have :

`m = (14 - - 7)/(21 - - 7) = (21)/(28) = (3)/(4)`

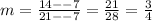
The equation of this line through (-7, -7) and (21, 14),is given by

`y-y_1=m(x-x_1)`

We substitute the point and slope to get:

`y - - 7 = (3)/(4) (x - - 7)`

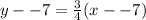
This gives us

`y = (3)/(4) x - (7)/(4)`

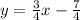
We check and see if the point (49,35) lies on the same line.

When x=49 do we get y=35?

`y = (3)/(4) * 49 - (7)/(4) = (147 - 7)/(4) = (140)/(4) = 35`

Yes

For point A (5,9)

When x=5, do we get y=9?

`y = (3)/(4) * 5 - (7)/(4) = (15 - 7)/(4) = (8)/(4) = 2 \\e9`

No

For point B (5,2)

When x=5, do we get y=2?

Yes, that's what we just got in A above.

For point C (17,11)

When x=17, do we get y=11?

`y = (3)/(4) * 17 - (7)/(4) = (51 - 7)/(4) = (46)/(4) \\e11`

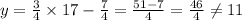
No

For point D (4,3)

When x=4, does y=3?

`y = (3)/(4) * 4 - (7)/(4) = (12 - 7)/(4) = (5)/(4) \\e \: 3`

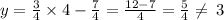
No

For point E (33,23)

When x=33, does y=23?

`y = (3)/(4) * 33 - (7)/(4) = (99 - 7)/(4) = (92)/(4) = 23`

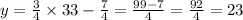
Yes