Answer:
Kevin's average swimming speed is 37.5 meters/minutes and speed of the lake's current is 12.5 meters/minutes.
Explanation:
Given:- Distance swim by Kevin = 200 metres
Time taken to swim against the lake current= 8 minutes.
Time taken to swim against the lake current=4 minutes.
To find:- average swimming speed of Kevin=?
Speed of the lakes current=?
Solution:-
Let, swimming speed of Kevin be x, and speed of lake current be y.
Therefore,
Speed of Kevin with lake current = x+y ---------------(1)
Speed of Kevin against lake current = x-y --------------(2)
Now formula to calculate speed is,
Speed =

Time
 Speed = Distance
Speed = Distance
Speed of Kevin with the lake current can be represented as,
Time
 Speed = Distance
Speed = Distance
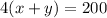 --------- (from 1 and given)
--------- (from 1 and given)
By dividing above equation with 4 we get,
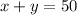 -----------------------(3)
-----------------------(3)
Speed of Kevin against the lake current can be represented as,
Time
 Speed = Distance
Speed = Distance
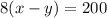
By dividing above equation with 8 we get,
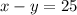 ---------------------(4)
---------------------(4)
By adding equation 3 and 4 we get,
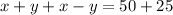
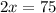

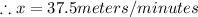 ---------------(5)
---------------(5)
Now substituting the value of x from equation 5 in equation 4,
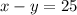
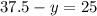
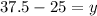
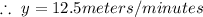
As x is the swimming speed of Kevin and y is the speed of lakes current,
Therefore Kevin's average swimming speed is 37.5 meters/minutes and speed of the lake's current is 12.5 meters/minutes.