Question

What is the midpoint and distance of
( -6 , 5), (-1 , -2)

Answer 1

The midpoint of given points is
`\left((-7)/(2), (3)/(2)\right)`

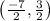
The distance between the given points is 8.6023 units

Solution:

Given that two points are (-6, 5) and (-1, -2)

We have to find the midpoint and distance

The midpoint of two given points is given as:

`m(x, y)=\left((x_(1)+x_(2))/(2), (y_(1)+y_(2))/(2)\right)`

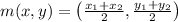
Here in this sum,

`x_(1)=-6 ; x_(2)=-1 ; y_(1)=5 ; y_(2)=-2`

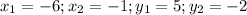
Substituting the values in formula, we get

`\begin{aligned}&m(x, y)=\left((-6+(-1))/(2), (5+(-2))/(2)\right)\\\\&m(x, y)=\left((-7)/(2), (3)/(2)\right)\end{aligned}`

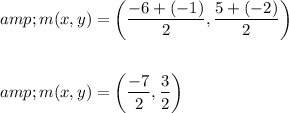
Thus the midpoint of given points is
`\left((-7)/(2), (3)/(2)\right)`

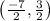
Distance between given points:

The formula for distance is given as:

`D=\sqrt{\left(x_(2)-x_(1)\right)^(2)+\left(y_(2)-y_(1)\right)^(2)}`

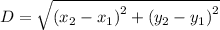
Substituting the values in formula, we get

`\begin{aligned}&D=\sqrt{\left(x_(2)-x_(1)\right)^(2)+\left(y_(2)-y_(1)\right)^(2)}\\\\&D=\sqrt{(-1-(-6))^(2)+(-2-5)^(2)}\\\\&D=\sqrt{5^(2)+(-2-5)^(2)}\\\\&D=√(25+49)=√(74)\end{aligned}`

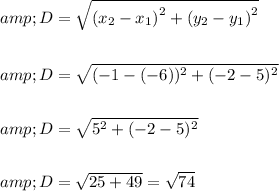
D = 8.6023 units

Thus the distance between the given points is 8.6023 units