Question

Can you simplify 6.05=0.65log(0.39) to 9.31=log(0.39)

This is done by dividing by .65, but I'm not sure if you can simplify a log like that.

Answer 1

The division rule of equality tells you that dividing both sides of the equation by the same (non-zero) number does not change the validity of the equation.

Explanation:

The equation can be divided by the coefficient of the log function without changing the value of the log function or its argument. Here, that means it is legitimate to divide both sides by 0.65. The result is approximately ...

9.3076923 = log(0.39)

Unless your problem statement tells you to round the number on the left side of this equation, you should maintain its full precision until you have the final answer to the problem at hand. Most useful scientific or graphing calculators will maintain 8 to 12 digit precision; a good one keeps 32 digits or more.

___

Comment on the equation

Of course, this logarithm must be to some base other than 10. We can write the logarithm as a log base "b" and solve for that base. Here, we'll use your value of 9.31 as a stand-in for the full-precision number, just so we don't have to write so many digits. We'll use the full-precision value in the final calculation.

`6.05=0.65\log_b{0.39}\\\\9.31\log{b}=\log{0.39}\\\\\log{b}=\frac{\log{0.39}}{9.31}\approx -0.0439\\\\b=10^(-0.0439)\approx 0.90378430`

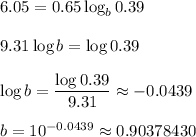
Your log equation is only true if the base of the logarithm is about 0.90378430.