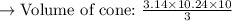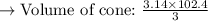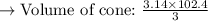Question

PLEASE HELP!! I FORGOT HOW TO DO THESE!:)

Answer 1

`107.18 \ \text{units}^(3)`

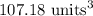
Explanation:

Reviewing the formula:

To find the volume of a cone, we need to use the formula
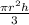`(\pi r^(2)h )/(3)`h" represents the height of the cone and "r" represents the radius of the cone.

`\text{Volume of cone:}\ (\pi r^(2)h )/(3)`

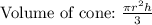
Reviewing the given information:

In the cone, we can see that the height of the cone is 10 units, and the radius of the cone is 3.2 units. Let's substitute the radius and the height of the cone to find the volume.

`\rightarrow \text{Volume of cone:}\ (3.14 * 3.2^(2) * 10 )/(3)`

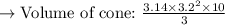
Finding the volume of the cone:

Now, simplify the expression.

`\rightarrow \text{Volume of cone:}\ (3.14 * 10.24 * 10 )/(3)`

`\rightarrow \text{Volume of cone:}\ (3.14 * 102.4)/(3)`

`\rightarrow \text{Volume of cone:}\ (3.14 * 102.4)/(3)`

`\rightarrow \boxed{\text{Volume of cone:} \ 107.18 \ \text{units}^(3)} \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (\text{Rounded to 2 decimal place})`