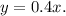Question

Point (5 5/8, 2 1/4) lies on a line that represents a proportional relationship. Write an equation for this relationship. What is the proportionality?

The point (6 1/2, y) also lies on the line. What is the y-coordinate of the point?

Answer 1

The equation is
`y=0.4x`

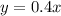
The y coordinate of point (6 1/2, y) is y=2 3/5

Explanation:

Let us first convert everything to decimal numbers:

`(5(5)/(8),2(1)/(4) )=(5.625,2.25)`

`6(1)/(2) =6.5`

In a proportional relationship

`(y_1)/(x_1) =(y_2)/(x_2)`

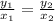
For the set of points
`(5(5)/(8),2(1)/(4) )`

`(y_1)/(x_1)=(2.25)/(5.625)=0.4`

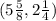
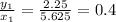
now this must equal
`(y_2)/(x_2)`:

`0.4=(y_2)/(x_2)=(y_2)/(6.5)\\y_2=0.4*6.5=2.6\:\:\:or\:as\:a\:mixed\:fraction\:\:\:2(3)/(5)`

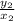Now for a proportional relationship the equation is

`y=kx`

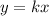
where
`k` is the common ratio between
`x` and
`y` (officially called the 'constant of proportionality').

Now in our case the common ratio is 0.4; therefore

`y=0.4x.`