Answer:
The we equation is

The constant of proportionality is

Explanation:
The given point is
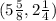
A proportional relationship has a general equation of the form:
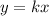
We substitute the point into the equation to get:

Change to improper fractions to get:
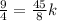
We multiply through by
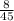
This gives us:
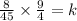

The equation is
