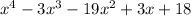Question

Find a polynomial of the specified degree that satisfies the given conditions. Degree 4; zeros −1, 1, 6 ; integer coefficients and constant term 18 f(x) =

Answer 1

`{x}^(4) - 3 {x}^(3) - 19 {x}^(2) + 3x + 18`

Explanation:

If a is a zero of a polynomial then

`(x - a)`

is a factor of the polynomial.

So since, -1, 1 ,6 are thr zeroes, then the factors is

`(x + 1)(x - 1)(x - 6)`

`( {x}^(2) - 1)(x - 6)`

`{x}^(3) - 6 {x}^(2) - x + 6`

We aren't done because we have a degree of 3 and a constant of 6.

Since we want a constant term 18, and a additional degree, we multiply by another binomial.

which will be

(x+3),

`({x}^(3) - 6 {x}^(2) - x + 6)(x + 3)`

`{x}^(4 ) - 6 {x}^(3) - {x}^(2) + 6x + 3 {x}^(3) - 18 {x}^(2) - 3x + 18`

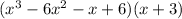
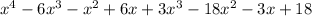
Which simplified gives us

`{x}^(4) -3 {x}^(3) - 19 {x}^(2) + 3x + 18`