Question

copy each expression below in simplify it using the order of operations a: 6+4(2+3)² b: (6+4)(2+3) c: 6+4x2³+3​

Answer 1

a:

6+4(5)^2 = 6 + 100 = 606

b:

(10)(5) = 50

c:

6+4x8+3 = 6+32+3 = 41

Answer 2

A. 106

B. 50

C. 41

Explanation:

a: 6+4(2+3)²

`\mathrm{Follow\:the\:PEMDAS\:order\:of\:operations}`

`6+4\cdot \:5^2`

`6+4\cdot \:25`

`6 + 100`

`106`

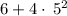
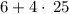
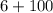
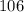
Hence, [A] = 106

~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

b: (6+4)(2+3)

`\mathrm{Follow\:the\:PEMDAS\:order\:of\:operations}`

`10\left(2+3\right)`

`10\cdot5`

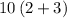
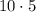
50

Hence, [B] = 50

~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

c: 6+4x2³+3​

`Follow\:the\:PEMDAS\:order\:of\:operations`

`6+4\cdot \:8+3`

`6+32+3`

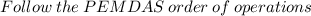
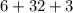
41

Hence, [C} = 41

~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

!Lenvy!