Answer:
The slopes are
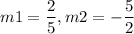
Therefore, the equations are equations of Perpendicular Lines .
Explanation:
Given:
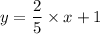 ......................Equation ( 1 )
......................Equation ( 1 )
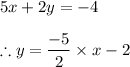 ..............Equation ( 2 )
..............Equation ( 2 )
To Find:
Slope of equation 1 = ?
Slope of equation 2 = ?
Solution:
On comparing with slope point form
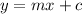
Where,
m = Slope
c = y-intercept
We get
Step 1.
Slope of equation 1 = m1 =

Step 2.
Slope of equation 1 = m2 =
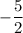
Step 3.
Product of Slopes = m1 × m2 =
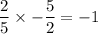
Product of Slopes = m1 × m2 = -1
Which is the condition for Perpendicular Lines
The slopes are
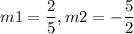
Therefore, the equations are equations of Perpendicular Lines .