Answer:
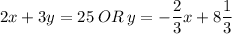
Explanation:
First, find the rate of change [slope]:
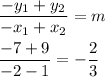
Now plug these coordinates into the Slope-Intercept Formula instead of the Point-Slope Formula, since it is much swifter that way. It does not matter which ordered pair you choose:
9 = ⅔ + b
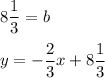
If you want it in Standard Form:
y = −⅔x + 8⅓
+ ⅔x + ⅔x
____________
⅔x + y = 8⅓ [We do not want fractions in our standard equation, so multiply by the denominator to get rid of it.]
3[⅔x + y = 8⅓]
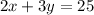
_______________________________________________
7 = −⅔[2] + b
−1⅓
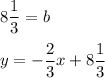
If you want it in Standard Form:
y = −⅔x + 8⅓
+ ⅔x + ⅔x
____________
⅔x + y = 8⅓ [We do not want fractions in our standard equation, so multiply by the denominator to get rid of it.]
3[⅔x + y = 8⅓]
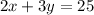
** You see? I told you that it did not matter which ordered pair you choose [as long your rate of change is correct] because you will ALWAYS get the exact same result.
I am joyous to assist you anytime.