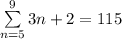Question

Evaluate the sum from n equals five to nine of quantity three n plus two

Answer 1

115

Explanation:

took test

Answer 2

The given expanded sum of the series is
`\sum\limits_(n=5)^(9)3n+2=115`

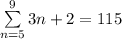
Explanation:

Given problem can be written as

`\sum\limits_(n=5)^(9)3n+2`

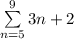
To find their sums:

Now expanding the series

That is put n=5,6,7,8,9 in the given summation

`\sum\limits_(n=5)^(9)3n+2=[3(5)+2]+[3(6)+2]+[3(7)+2]+[3(8)+2]+[3(9)+2]`

`=[15+2]+[18+2]+[21+2]+[24+2]+[27+2]`

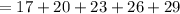`=17+20+23+26+29` (adding the terms)

`=115`

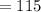
Therefore
`\sum\limits_(n=5)^(9)3n+2=115`

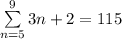
Therefore the given sum of the series is
`\sum\limits_(n=5)^(9)3n+2=115`

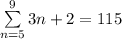
The given expanded sum of the series is
`\sum\limits_(n=5)^(9)3n+2=115`