Answer:
Total possible sequences of rolls is 20.
Explanation:
A standard six-sided die is rolled $5$ times.
It is given that you are told that among the rolls, there was one $4,$ one $5,$ and three $6$'s.
We need to find possible sequences of rolls could there have been.
Total numbers to arrange (i.e.,4,5,6,6,6)= 5
Repleted numbers (i.e., 6,6,6) = 3
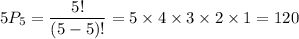
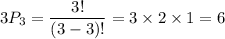
Total possible ways are

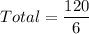

Therefore, the total possible sequences of rolls is 20.