Question

A billiard ball is struck by a cue. It travels 100 cm before ricocheting off a rail and traveling another 120 cm into a corner pocket. The angle between the path as the ball approaches the rail and the path after it strikes the rail is 45 degrees. How far is the corner pocket from where the cue initially struck the ball?

Answer 1

86 cm

Explanation:

We are given that

Billiard ball travels before ricocheting off a rail=100 cm

After ricocheting ball travels=120 cm

The angles between the path as the ball approaches the rail and the path after strikes the rail=45 degrees

We have to find the distance between corner pocket from where cue initially struck the ball.

Cosine law:
`c^2=√(a^2+b^2-abcos\theta)`

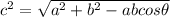
By using cosine law

`AB=√(AC^2+BC^2-2(AC)(BC)Cos45)`

`AB=\sqrt{(100)^2+(120)^2-2(100)(120)* (1)/(\sqrt 2)}`

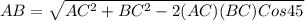
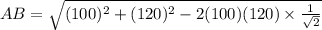
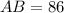`AB=86`cm

Hence, the distance of cornet pocket form where the cue initially struck the ball=86 cm