Answer:
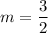
Explanation:
Given points are: ( 1 , 3 ) , ( 2 , 3 ) and ( 3 , 6 )
The average of x-coordinate will be:
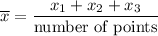
1) Finding
- Average of the x coordinates:
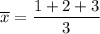
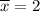
- Average of the y coordinates:
similarly for y
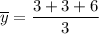

2) Finding the line through
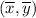 with slope m.
with slope m.
Given a point and a slope, the equation of a line can be found using:
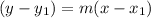
in our case this will be
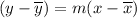
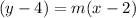
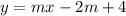
this is our equation of the line!
3) Find the squared vertical distances between this line and the three points.
So what we up till now is a line, and three points. We need to find how much further away (only in the y direction) each point is from the line.
- Distance from point (1,3)
We know that when x=1, y=3 for the point. But we need to find what does y equal when x=1 for the line?
we'll go back to our equation of the line and use x=1.
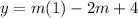

now we know the two points at x=1: (1,3) and (1,-m+4)
to find the vertical distance we'll subtract the y-coordinates of each point.
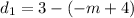
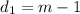
finally, as asked, we'll square the distance

- Distance from point (2,3)
we'll do the same as above here:

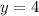
vertical distance between the two points: (2,3) and (2,4)
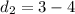
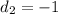
squaring:
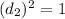
- Distance from point (3,6)
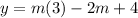
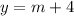
vertical distance between the two points: (3,6) and (3,m+4)
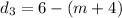
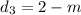
squaring:
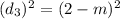
3) Add up all the squared distances, we'll call this value R.
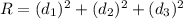
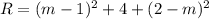
4) Find the value of m that makes R minimum.
Looking at the equation above, we can tell that R is a function of m:
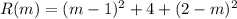
you can simplify this if you want to. What we're most concerned with is to find the minimum value of R at some value of m. To do that we'll need to derivate R with respect to m. (this is similar to finding the stationary point of a curve)
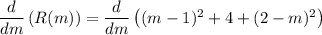
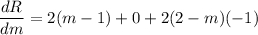
now to find the minimum value we'll just use a condition that
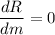

now solve for m:
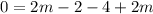
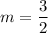
This is the value of m for which the sum of the squared vertical distances from the points and the line is small as possible!