Question

[(a/b)+1] / (c/b)

In the expression above, a, b and c are different numbers and each is one of the numbers 2, 3 or 5.
What is the greatest possible value of the expression?

A) 8/3 B) 4 C) 9/2 D) 5 E) 6

Answer 1

B) 4

Explanation:

To find what values of a,b and c should be 2,3 and 5 such that the expression results in the greatest value possible.

We need to first simplify the expression, so that we can easily understand it.

`((a)/(b)+1)/((c)/(b))`

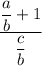
firstly, just break apart the fractions so we have two separate fractions instead one long fraction.

`((a)/(b)+1)/((c)/(b))`

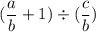
division and multiplication are reciprocal to each other!

`((a+b)/(b))*((b)/(c))\\`

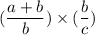
finally the b's cancel out, making our problem even simpler.

`(a+b)/(c)`

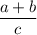
Now, in order to have this expression give the largest possible value, we'll need to have:

1. the larger values at the numerator i.e (3,5)
2. smaller values at the denominator i.e (2)

`(a+b)/(c)`

`(3+5)/(2)`

`(8)/(2)=4`

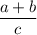
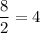
so B) 4 is the right answer!