Question

Let $$X_1, X_2, ...X_n$$ be uniformly distributed on the interval 0 to a. Recall that the maximum likelihood estimator of a is $$a = max(X_i)$$. Argue intuitively why aˆ cannot be an unbiased estimator for a. b. Suppose that E(a) = na/(n + 1). Is it reasonable that aˆ consistently underestimates a? Show that the bias in the estimator approaches zero as n gets large. c. Propose an unbiased estimator for a. d. Let $$Y = max(X_i)$$. Use the fact that Y ≤ y if and only if each $$X_i ≤ y$$ to derive the cumulative distribution function of Y . Then show that the probability density function of Y is. $$f(y) = [ny^n - ^1/a^n 0$$, 0 ≤ y ≤ a otherwise, Use this result to show that the maximum likelihood estimator for a is biased. e. We have two unbiased estimators for a: the moment estimator $$a_1=2\overline{\mbox{X}}$$ and $$a_2 = [(n + 1)/n] max(X_i)$$, where max $$(X_i)$$ is the largest observation in a random sample of size n. It can be shown that $$V(a_1) = a^2/(3n)$$ and that $$V(a_2) = a^2/[n(n + 2)]$$. Show that if n > 1, aˆ2 is a better estimator than aˆ. In what sense is it a better estimator of a?

Answer 1

a)
`\hat a = max(X_i)`

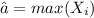
For this case the value for
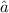`\hat a` is always smaller than the value of a, assuming
`X_i \sim Unif[0,a]` So then for this case it cannot be unbiased because an unbiased estimator satisfy this property:

`E(a) - a= 0` and that's not our case.

b)
`E(\hat a) - a= (na)/(n+1) - a = (na -an -a)/(n+1)= (-a)/(n+1)`

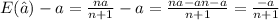
Since is a negative value we can conclude that underestimate the real value a.

`\lim_( n \to\infty) -(1)/(n+1)= 0`

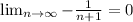
c)
`P(Y \leq y) = P(max(X_i) \leq y) = P(X_1 \leq y, X_2 \leq y, ..., X_n\leq y)`

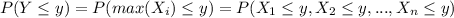
And assuming independence we have this:

`P(Y \leq y) = P(X_1 \leq y) P(X_2 \leq y) .... P(X_n \leq y) = [P(X_1 \leq y)]^n = ((y)/(a))^n`

`f_Y (Y) = n ((y)/(a))^(n-1) * (1)/(a)= (n)/(a^n) y^(n-1) , y \in [0,a]`

e) On this case we see that the estimator
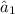`\hat a_1` is better than
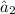`\hat a_2` and the reason why is because:

`V(\hat a_1) > V(\hat a_2)`

`(a^2)/(3n)> (a^2)/(n(n+2))`

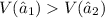
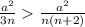
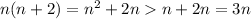`n(n+2) = n^2 + 2n > n +2n = 3n` and that's satisfied for n>1.

Explanation:

Part a

For this case we are assuming
`X_1, X_2 , ..., X_n \sim U(0,a)`

And we are are ssuming the following estimator:

`\hat a = max(X_i)`

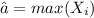
For this case the value for
`\hat a` is always smaller than the value of a, assuming
`X_i \sim Unif[0,a]` So then for this case it cannot be unbiased because an unbiased estimator satisfy this property:

`E(a) - a= 0` and that's not our case.

Part b

For this case we assume that the estimator is given by:

`E(\hat a) = (na)/(n+1)`

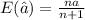
And using the definition of bias we have this:

`E(\hat a) - a= (na)/(n+1) - a = (na -an -a)/(n+1)= (-a)/(n+1)`

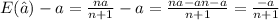
Since is a negative value we can conclude that underestimate the real value a.

And when we take the limit when n tend to infinity we got that the bias tend to 0.

`\lim_( n \to\infty) -(1)/(n+1)= 0`

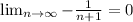
Part c

For this case we the followng random variable
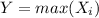`Y = max (X_i)` and we can find the cumulative distribution function like this:

`P(Y \leq y) = P(max(X_i) \leq y) = P(X_1 \leq y, X_2 \leq y, ..., X_n\leq y)`

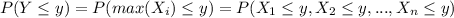
And assuming independence we have this:

`P(Y \leq y) = P(X_1 \leq y) P(X_2 \leq y) .... P(X_n \leq y) = [P(X_1 \leq y)]^n = ((y)/(a))^n`

Since all the random variables have the same distribution.

Now we can find the density function derivating the distribution function like this:

`f_Y (Y) = n ((y)/(a))^(n-1) * (1)/(a)= (n)/(a^n) y^(n-1) , y \in [0,a]`

Now we can find the expected value for the random variable Y and we got this:

`E(Y) = \int_(0)^a (n)/(a^n) y^n dy = (n)/(a^n) (a^(n+1))/(n+1)= (an)/(n+1)`

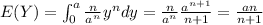
And the bias is given by:

`E(Y)-a=(an)/(n+1) -a=(an-an-a)/(n+1)= -(a)/(n+1)`

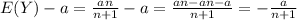
And again since the bias is not 0 we have a biased estimator.

Part e

For this case we have two estimators with the following variances:

`V(\hat a_1) = (a^2)/(3n)`

`V(\hat a_2) = (a^2)/(n(n+2))`

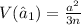
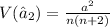
On this case we see that the estimator
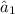`\hat a_1` is better than
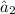`\hat a_2` and the reason why is because:

`V(\hat a_1) > V(\hat a_2)`

`(a^2)/(3n)> (a^2)/(n(n+2))`

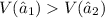
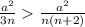
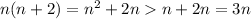`n(n+2) = n^2 + 2n > n +2n = 3n` and that's satisfied for n>1.