Answer:
The rate rate of change of radius is
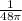 inches per second when the diameter is 12 inches.
inches per second when the diameter is 12 inches.
The radius is changing more rapidly when the diameter is 12 inches.
Explanation:
Consider the provided information.
A spherical balloon is being inflated at a rate of 3 cubic inches per second.
The volume of sphere is
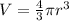
Differentiate the above formula with respect to time.
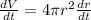
Substitute the respective values in the above formula,
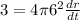
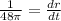
The rate rate of change of radius is
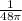 inches per second when the diameter is 12 inches.
inches per second when the diameter is 12 inches.
When d=16


Thus, the radius is changing more rapidly when the diameter is 12 inches.