Question

A rectangular area against a wall is to be fenced off on the other three sides to enclose 800 square feet. What are the dimensions that is will result in the least amount of fencing?

Answer 1

The length of 20 feet and width of 40 feet will result in the least amount of fencing.

Explanation:

Please find the attachment.

Let w represent width and l represent length of the rectangle.

We have been given that a rectangular area against a wall is to be fenced off on the other three sides to enclose 800 square feet.

We know that area of rectangle is width times length that is:

`A=w\cdot l`

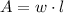
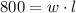`800=w\cdot l` This is our constraint equation.

We can see from the attachment that the fencing would be for 3 sides that is:

`\text{Perimeter}=l+l+w`

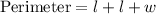
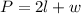`P=2l+w` This is our objective equation.

From constraint equation, we will get:

`w\cdot l=800`

`w=(800)/(l)`

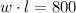
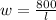
Substitute this value in objective equation:

`P=2l+(800)/(l)`

`P=2l+800l^(-1)`

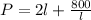
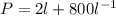
Let us find the derivative of objective equation.

`P'=2-800l^(-2)`

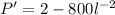
Now, we will set the derivative equal to 0 to solve for length:

`2-800l^(-2)=0`

`2-(800)/(l^2)=0`

`-(800)/(l^2)=-2`

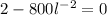
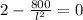
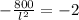
Cross multiply:

`-2l^2=-800`

`(-2l^2)/(-2)=(-800)/(-2)`

`l^2=400`

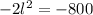
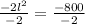
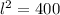
Take positive square root:

`l=√(400)`

`l=20`

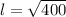
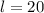
Upon substituting
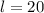`l=20` in
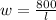`w=(800)/(l)`, we will get:

`w=(800)/(20)`

`w=40`

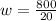
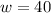
Therefore, the length of 20 feet and width of 40 feet will result in the least amount of fencing.