Question

A researcher would like to estimate the proportion of all children that have been diagnosed with Autism Spectrum Disorder (ASD) in their county. They are using 95% confidence level and the CDC national estimate that 1 in 68 ≈ 0.0147 children are diagnosed with ASD. What sample size should the researcher use to get a margin of error to be within 2%? Round up to the nearest integer.

Answer 1

Sample size of at least 139 children is required.

Explanation:

We are given that the a researcher would like to estimate the proportion of all children that have been diagnosed with Autism Spectrum Disorder (ASD) in their country.

Let p = proportion of children diagnosed with ASD = 1/68 = 0.0147

Also, Margin of error = 3%

Confidence level = 95%

Margin of error formula =
`Z_(\alpha)/(2) *(\sigma)/(√(n) )`

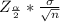
where,
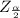`Z_(\alpha)/(2)` = At 5% level of significance z score has value of 1.96

`\sigma` =
`√(p(1-p))` =
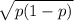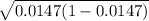`√(0.0147(1-0.0147))` = 0.1203

So, Margin of error =
`1.96 *(√(0.0147*(1-0.0147)) )/(√(n) )`

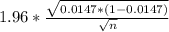
0.02 =
`1.96 *(0.1203 )/(√(n) )`

n =
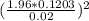`((1.96*0.1203)/(0.02))^(2)` = 139.10 ≈ 139.

Therefore, the researcher must use a sample size of at least 139 children to get a margin of error to be within 2%.

Answer 2

The researcher should use a sample size of at least 140 children to get a margin of error to be within 2%.

Explanation:

In a sample with a number n of people surveyed with a probability of a success of
`\pi`, and a confidence interval
`1-\alpha`, we have the following confidence interval of proportions.

`\pi \pm z\sqrt{(\pi(1-\pi))/(n)}`

In which

z is the zscore that has a pvalue of
`1 - (\alpha)/(2)`.

`M = z\sqrt{(\pi(1-\pi))/(n)}` is the margin of error.

95% confidence interval

So
`\alpha = 0.05`, z is the value of Z that has a pvalue of
`1 - (0.05)/(2) = 0.975`, so
`z = 1.96`.

We have that:

`M = 0.02, \pi = 0.0147`

So

`M = z\sqrt{(\pi(1-\pi))/(n)}`

`0.02 = 1.96\sqrt{(0.0147*(1-0.0147))/(n)}`

`0.02√(n) = 0.2359`

`√(n) = 11.79`

`n = 139.1`

The researcher should use a sample size of at least 140 children to get a margin of error to be within 2%.