Answer:
Sample size of at least 514 Americans is required.
Explanation:
We are given that the soap taste is inherited through the olfactory receptor gene OR6A2. About 14% of the population has this gene.
Let p = % of population having this gene = 0.14
Also, Margin of error = 3%
Confidence level = 95%
Margin of error formula =

where,
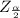 = At 5% level of significance z score has value of 1.96
= At 5% level of significance z score has value of 1.96
 =
=
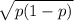 =
=
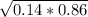 = 0.347
= 0.347
So, Margin of error =
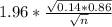
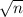 =
=
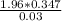
n =
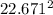 = 513.95 ≈ 514
= 513.95 ≈ 514
Therefore, sample must be of 514 Americans .