Answer: b. 0.98
Explanation:
The formula to find the maximum error of the estimated mean :
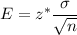 (1)
(1)
, where
 = standard deviation
= standard deviation
n= Sample size
z* = Critical z-value.
As per given , we have
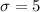
n=100
Critical value for 95% confidence interval = z*=1.96
Put these values in the formula (1), we get
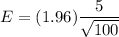
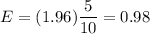
Hence, the maximum error of the estimated mean quality for a 95% level of confidence is 0.98.
Therefore , the correct answer is b. 0.98 .