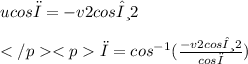Answer:
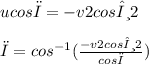
Step-by-step explanation:
Two identical sticky masses m are moving in the xy-plane, with their momenta at an angle of φ with one another. They are each moving at the same speed v when they collide at the origin of the coordinates and stick together. After the collision, the masses move at an angle −θ2 with respect to the +x axis at speed v2 .1. What was the angle φ?
from the principle of momentum
In a system of colliding bodies,we know that the total momentum before collision will equal to the total momentum after collision.
Take note that momentum is the product of mass and velocity
momentum before collision=momentum after collision
mass, m
u=initial velocity of the identical masses
v2=the common velocity after the collision
Note that the collision is inelastic , since they both moved with the same velocity
umcosφ+umcosφ=(m+m)v2cos−θ2
2mucosφ=2mv2cos−θ2