Answer:
a)
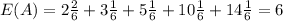
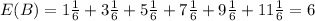
b)

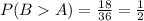
c) (i)
If the goal is to obtain a higher score than an opponent rolling the other die, It's better to select the die B because the probability of obtain higher score than an opponent rolling the other die is more than for the die A. Since P(B>A) > P(A>B)
(ii)
We see that the expected values of both the dies A and B were equal, so then a roll of any of the two dies would get us the maximum value required.
Explanation:
Previous concepts
Normal distribution, is a "probability distribution that is symmetric about the mean, showing that data near the mean are more frequent in occurrence than data far from the mean".
The expected value of a random variable X is the n-th moment about zero of a probability density function f(x) if X is continuous, or the weighted average for a discrete probability distribution, if X is discrete.
The variance of a random variable X represent the spread of the possible values of the variable. The variance of X is written as Var(X).
Solution to the problem
Part a
For this case we can use the following formula in order to find the expected value for each dice.
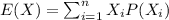
Die A has 2 twos, 1 three, 1 five, 1 ten, and 1 fourteen on its faces. The total possibilites for die A ar 2+1+1+1+1= 6
And the respective probabilites are:
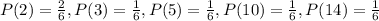
And if we find the expected value for the Die A we got this:
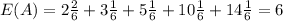
Die B has a one, a three, a five, a seven, a nine, and an eleven on its faces
And the respective probabilites are:

And if we find the expected value for the Die A we got this:
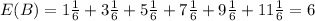
Part b
Let A be the event of a number showing on die A and B be the event of a number showing on die B.
For this case we need to find P(B>Y) and P(B>A).
First P(A>B):
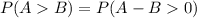
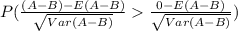
We can solve this using the sampling space for the experiment on this case we have 6*6 = 36 possible options for the possible outcomes and are given by:
S= {(2,1),(2,3),(2,5),(2,7),(2,9),(2,11), (2,1),(2,3),(2,5),(2,7),(2,9),(2,11), (3,1),(3,3),(3,5),(3,7),(3,9),(3,11), (5,1)(5,3),(5,5),(5,7),(5,9),(5,11), (10,1),(10,3),(10,5),(10,7),(10,9),(10,11), (14,1),(14,3),(14,5),(14,7),(14,9), (14,11)}
We need to see how in how many pairs the result for die A is higher than B, and we have: (2,1), (2,1), (3,1), (5,1), (5,3), (10,1), (10,3), (10,5), (10,7), (10,9), (14,1), (14,3),(14,5),(14,7),(14,9), (14,11). so we have 16 possible pairs out of the 36 who satisfy the condition and then we have this:

And for the other case when B is higher than A we have this: (2,3), (2,5), (2,7), (2,9), (2,11), (2,3), (2,5), (2,7), (2,9), (2,11), (3,5), (3,7), (3,9), (3,11), (5,7), (5,9), (5,11), (10,11). We have 18 possible pairs out of the 36 who satisfy the condition and then we have this:
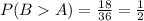
Part c
(i)
If the goal is to obtain a higher score than an opponent rolling the other die, It's better to select the die B because the probability of obtain higher score than an opponent rolling the other die is more than for the die A. Since P(B>A) > P(A>B)
(ii)
We see that the expected values of both the dies A and B were equal, so then a roll of any of the two dies would get us the maximum value required.