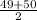Answer:
Explanation:
Let us consider two the numbers be a and b.
Avg. of the two digits =
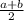
If it is (a.b) , then the actual value of the number is (if you see 21.45, you get it by 21 +45/100)
∴equating =
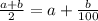
On solving this equation, we get 50a = 49b
We can now write this as
a = 49b - 49a
∴ a = 49 ( b - a )
This tells us a few things. First, b - a has to be a positive value, because it can't be 0 other wise a would become 0.
It cannot be negative because then a would be negative .. and we know, a is a 2 digit positive integer.
∴ b > a ..
Also, if you notice .. whatever value ( b - a ) is equal to .. say 1, 2, 3, say 15 .. whatever ...
a will always be a multiple of 49 ..
because a will be 49 × ( 1 or 2 or 3 or say 15 .. )
That means, a has to be a multiple of 49.
That said, there are only 2 such numbers within 100 which are multiples of 49.
One is 49 itself, the other is 98.
So now we have some idea , as to what a can be .. it can be either 49 or 98.
Lets start with the assumption that a = 98. What happens then ?
We know b > a .. so it means b has to be a value less than 100 but greater than 98.
The only such value is 99. ∴ We get b = 99.
But if you do the math, = 98.50 .. it doesn't satisfy the second condition, "obtained by writing one of the two-digit integers before the decimal point and the other two-digit integer after the decimal point."
So that means, a = 49 for sure.
Now that we know a, its easy to find b from :
50a = 49b
∴ b = 50
If you test it out,