Answer:
a) There is a 75% probability that the freshman is enrolled in both English 105 and Mathematics 101.
b) There is a 15% probability that the freshman is enrolled in English 105 but not in Mathematics 101.
c) 93.75% probability that the freshman is also enrolled in English 105
Explanation:
We solve this problem building the Venn's diagram of these percentages.
I am going to say that:
A are those freshmen enrolled in English 105.
B are those freshman Enrolled in Mathematics 101.
We have that:
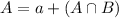
In which a is the probability that a freshmen is enrolled in English 105 but not in Mathematics 101 and
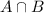 is the probability that a freshmen is enrolled in both these classes.
is the probability that a freshmen is enrolled in both these classes.
By the same logic, we have that:
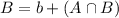
Solution
90% of the freshmen are enrolled in English 105
So A = 0.9
80% are enrolled in Mathematics 101
So B = 0.8
5% are enrolled in Mathematics 101 but not in English 105.
So b = 0.05
a. What is the probability that the freshman is enrolled in both English 105 and Mathematics 101?
This is
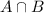 .
.
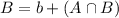
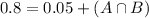
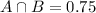
There is a 75% probability that the freshman is enrolled in both English 105 and Mathematics 101.
b. What is the probability that the freshman is enrolled in English 105 but not in Mathematics 101?
This is a.
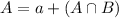
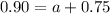
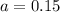
There is a 15% probability that the freshman is enrolled in English 105 but not in Mathematics 101.
c. Suppose the freshman chosen is known to be enrolled in Mathematics 101. What is the probability that the freshman is also enrolled in English 105?
This is
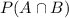 divided by P(B). So 0.75/0.8 = 0.9375.
divided by P(B). So 0.75/0.8 = 0.9375.
There is a 93.75% probability that the freshman is also enrolled in English 105